Modelos matemáticos aplicados a la epidemia
Prof. Augusto Rangel
La presente sección realiza una recopilación de los modelos matemáticos que pueden ser aplicados para representar el crecimiento de la pandemia, así como se presenta un artículo sobre la proyección de las cifras futuras a nivel estadístico.
Click en el siguiente enlace para ir al artículo y observar las proyecciones.
Conceptos básicos
En la presente investigación se hace uso de los modelos matemáticos como una herramienta para el entendimiento de cómo se transmiten las enfermedades infecciosas. Los objetivos fundamentales de formular dichos modelos matemáticos son describir y predecir información sobre lo que sucederá, de forma aproximada. Se busca proveer un medio que posibilite la comprensión de la dispersión del COVID-19 a través de la población.
Para acceder a la sección de cálculo de infectados, recuperados y fallecidos, click aquí.
Los modelos matemáticos se clasifican en: determinísticos y estocásticos.
- Cuando se habla de un modelo determinístico, es posible controlar los factores implicados en el estudio y, por tanto, sus resultados se pueden predecir de manera exacta.
- Un modelo estocástico, por su parte, posee factores variables que intervienen en el estudio; no es posible controlar dichos factores, por lo tanto, no se producen resultados exactos.
Número reproductivo básico
Técnicamente pronunciada como “erre subcero”, esta representa el número de nuevas infecciones que se calcula que provienen de un solo caso. Dicho de otro modo, si el R0 de una enfermedad es de 2,5, entonces, se espera que una persona enferma infecte, en promedio, a 2,5 más.
Un R0 menor a 1 sugiere que el número de casos se está reduciendo, lo cual podría permitir que ciertas sociedades reanuden sus actividades. Un R0 mayor a 1 indica que el número de casos está aumentando, lo cual tal vez requiera nuevos cierres de emergencia u otras medidas.
Modelo SIR/
Este modelo parte de la premisa en la que los individuos en estudio se encuentran en uno de tres estados posibles. En base a ello, cada individuo se puede clasificar dentro de las categorías: Susceptibles (S), Infectados (I) y Removidos (R). Se asume que la interacción entre los individuos es aleatoria.
S = SUSCEPTIBLES. Aquellos individuos capaces de ser contagiados.
I = INFECTADOS. La población que ya está infectada con la enfermedad.
R = REMOVIDOS. Aquellas personas que tuvieron la enfermedad, y ya no pueden contagiarla por una de dos causas: se recuperaron satisfactoriamente, o fallecieron.
El estado chileno se encuentra manejando este sistema para medir el impacto de la pandemia. Información sobre ello se puede encontrar en el artículo “Evolución de las epidemias: La Matemática de aislarse”, de los investigadores Héctor Pastén (Facultad de Matemáticas UC) y Jorge Castillo (Z Data Lab).
Los doctores en matemática agregan que "el llamado modelo SIR es un modelo matemático desarrollado en 1927 y que hasta el día de hoy es la base para otros modelos más sofisticados en el estudio de epidemias. SIR toma en cuenta aspectos de la propagación de una epidemia, que el modelo exponencial no considera: que después de un cierto tiempo, los enfermos se recuperan (o lamentablemente, fallecen) y dejan de ser contagiosos (al menos por un tiempo); que mientras más infectados hay, menos personas sanas quedan susceptibles de ser contagiadas”, sostienen.
Duván Henao y Gregorio Moreno insisten en que el modelo SIR, en su forma más sencilla, “es un sistema de tres ecuaciones diferenciales relacionando la cantidad de personas en estos tres grupos y cómo varían a través del tiempo”.
La representación de los susceptibles, infectados y recuperados, se realiza de la siguiente manera en el modelo SIR:
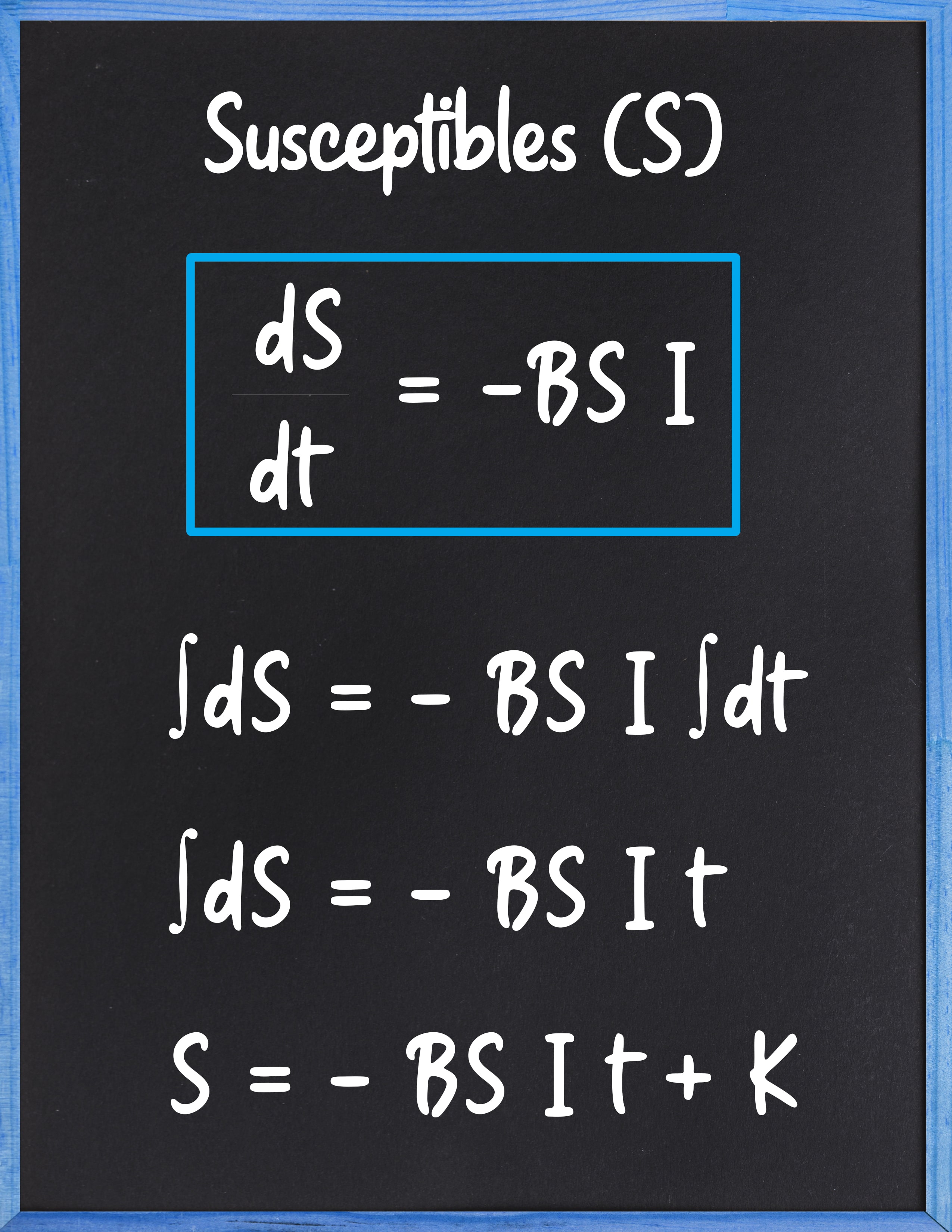
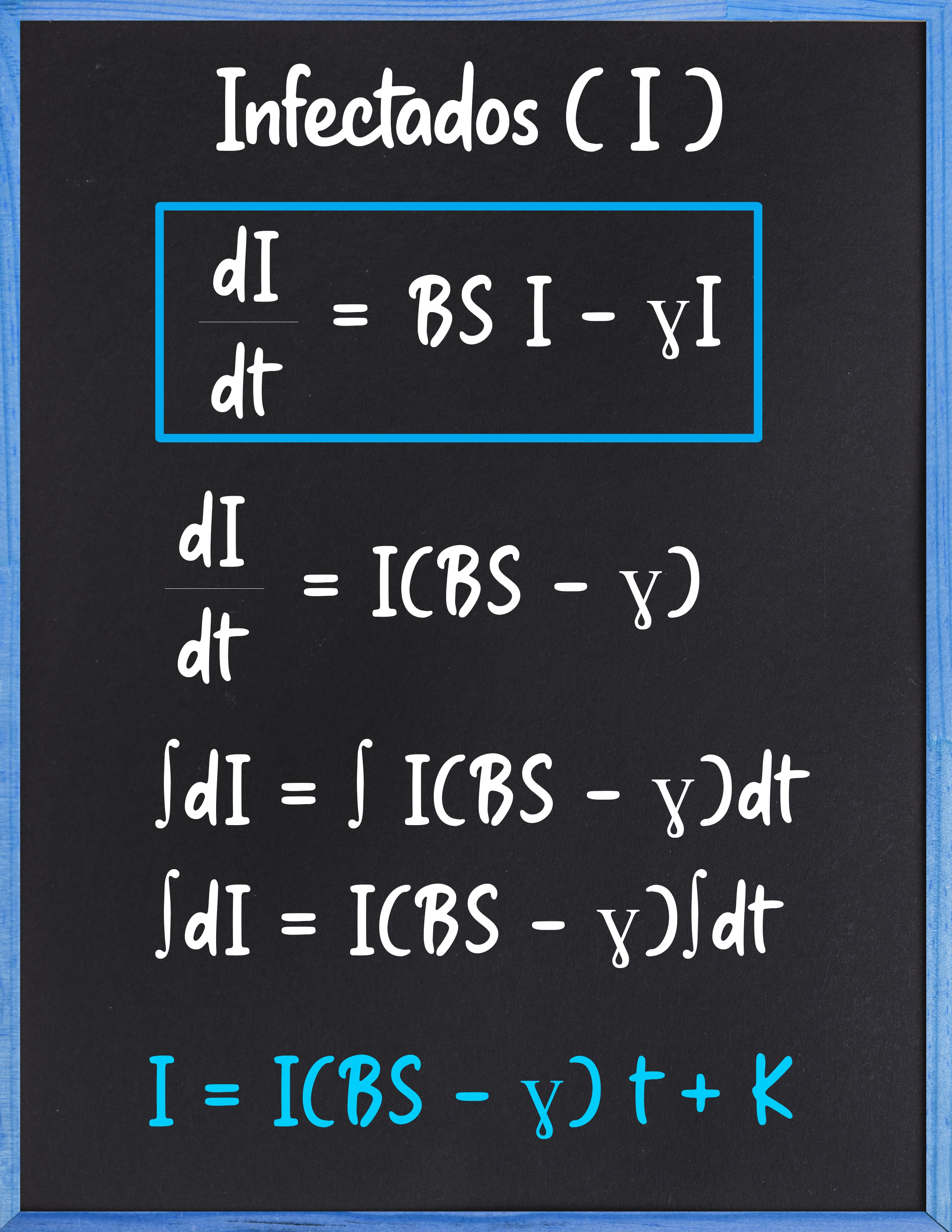

A partir del modelado I, es posible obtener la fórmula básica:

Es posible tener en cuenta, además, a la ecuación logística:

Se tiene:


Aplicación del modelo SIR para un caso determinado (ejemplo)
Un colegio tiene 1000 alumnos y tiene 1 infectado, a los 4 días vamos a tener 50 infectados. ¿Cuántos infectados vamos a tener a los 6 días?
S = 1000 K
Io = 1
B = K
In(4) = 50 infectados
In(6) = ?
In(t) = Infectados +- días
El procedimiento a seguir sería el siguiente:

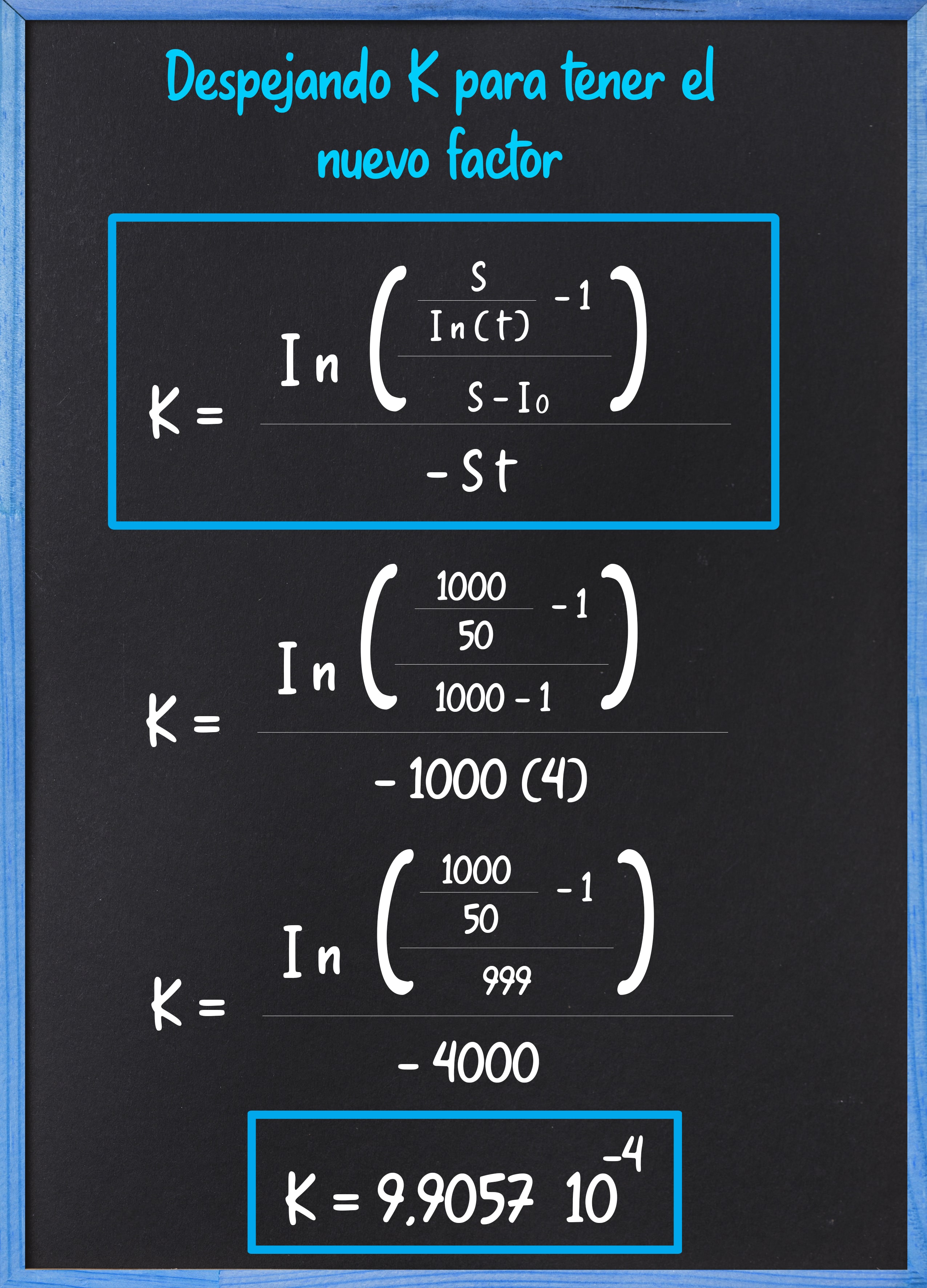


Otros modelos
Con el fin de estudiar el comportamiento de la pandemia, es posible utilizar otras formas, basadas en el modelo exponencial.


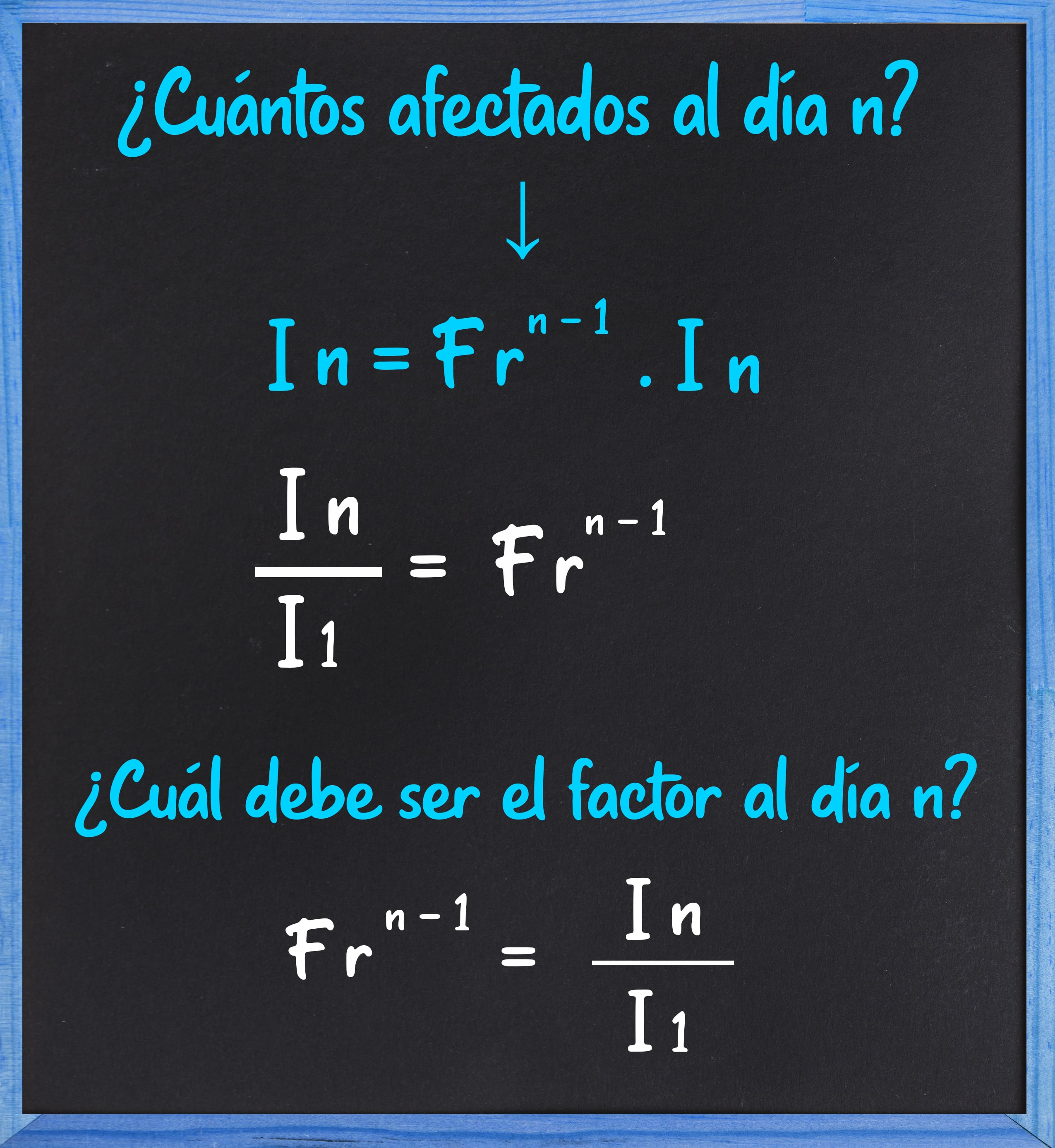

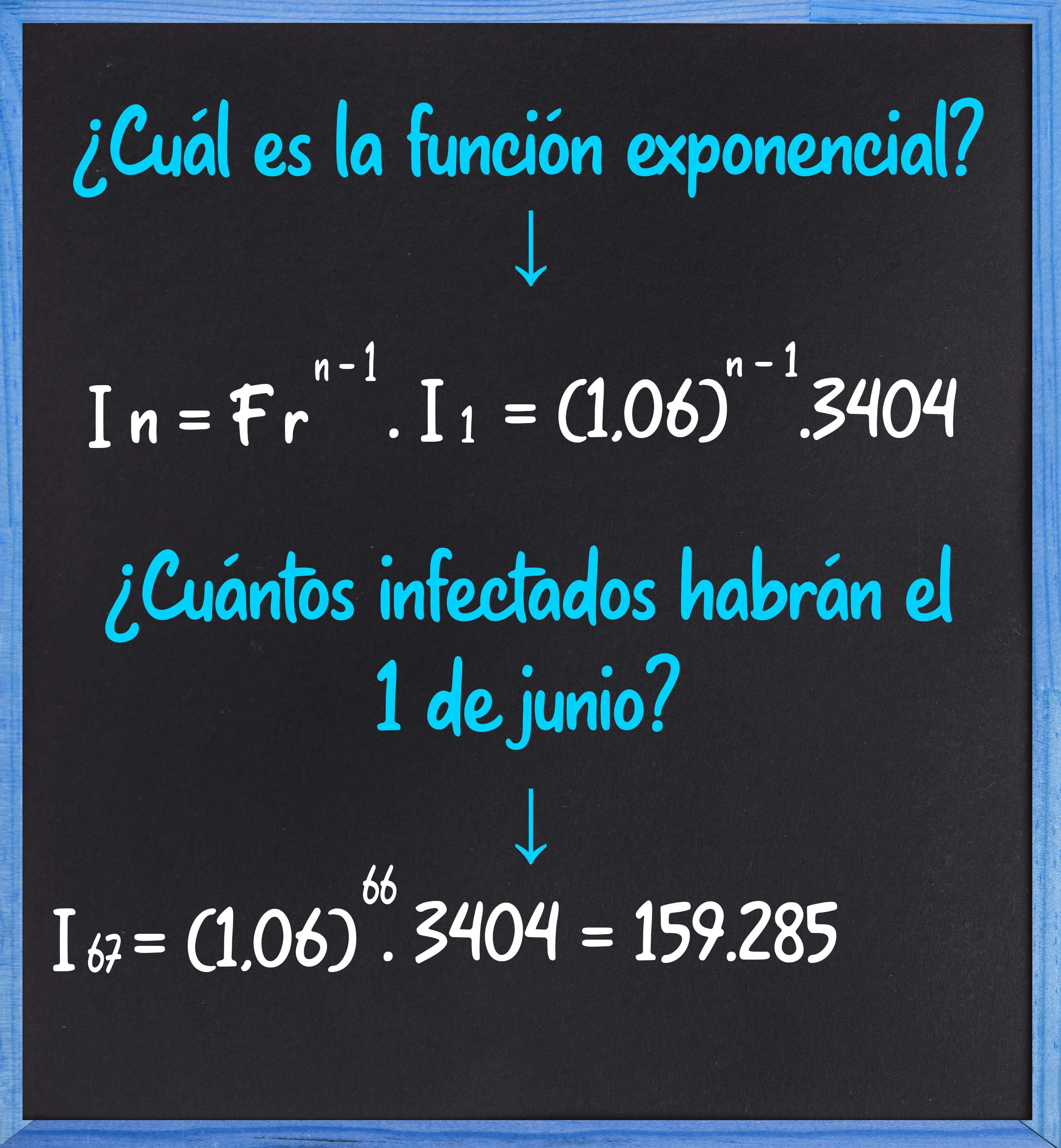
Análisis del COVID-19 en Chile. Ejemplo y cálculo automático de cifras proporcionadas
Tomando como factor de riesgo el número 1,1, se evalúa el comportamiento de los datos a partir del 1ero de abril con 3404.
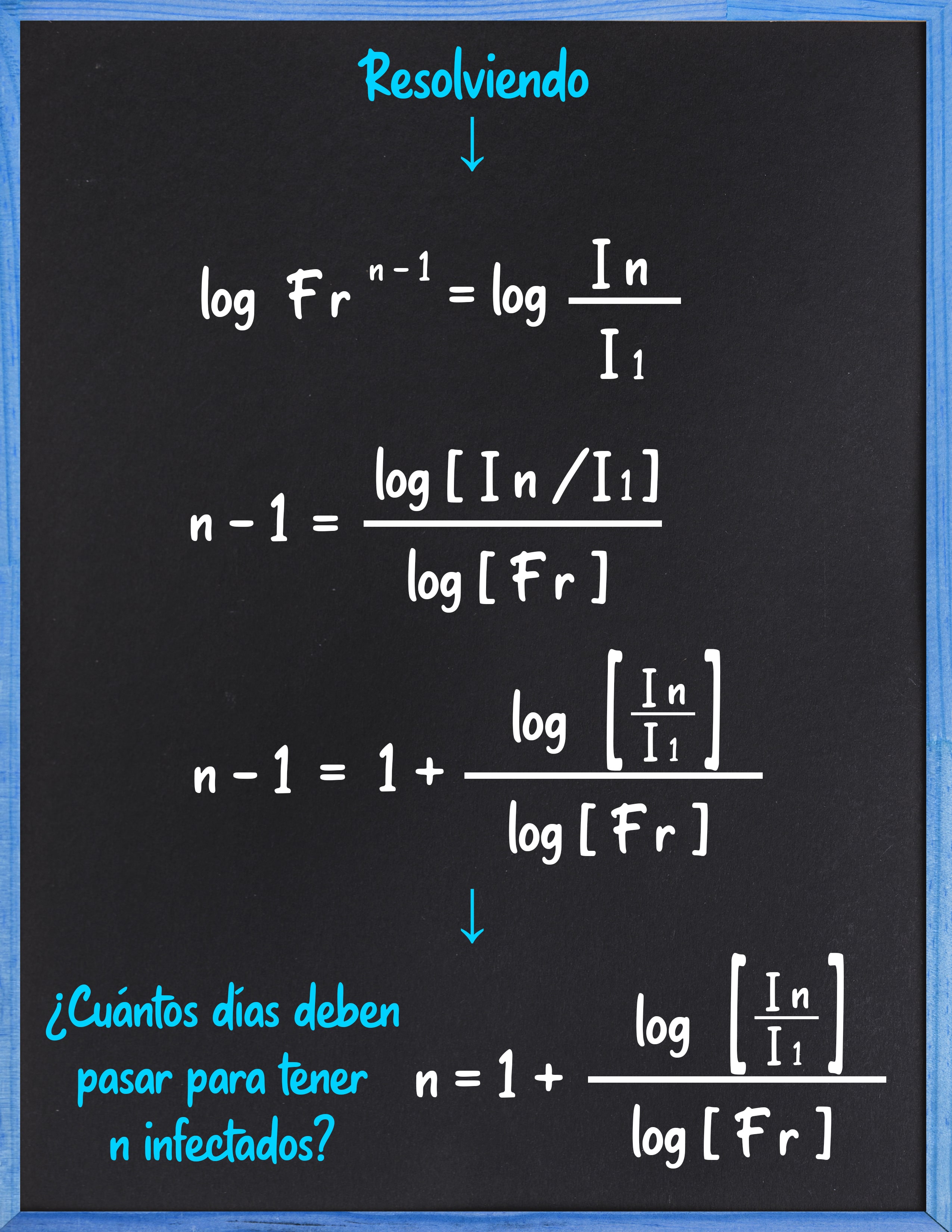
Calculador de casos para el día n
Categoría

¿Cuántos días deben pasar para tener n casos?
Categoría

Calculador del factor para que el día n haya determinada cantidad de casos
Categoría
Proyecciones netamente estadísticas del coronavirus (contagiados y fallecidos)
- - Es importante destacar que la finalidad del presente artículo es informar sobre una manera de realizar la proyección de las cifras de contagiados y fallecidos del COVID-19 de forma estadística; esto significa, que las cifras expuestas no necesariamente deben ser exactas, pero sí cercanas a la realidad.
- - Se hace necesario además mencionar que las cifras dadas en los cuadros referentes al caso Chile pueden variar dependiendo de la llegada del peak de contagiados y fallecidos. Al llegar el peak, las cifras diarias disminuirán gradualmente (no así el acumulado, que seguirá incrementando), y por lo tanto, los datos expuestos en los cuadros al final de este artículo van a variar.
- - Se considera que el peak (punto de inflexión) ha llegado cuando pasan 5 a 6 días consecutivos donde las cifras diarias van disminuyendo, y no vuelven a aumentar durante los días posteriores.
- - En este artículo no se toman en cuenta los recuperados, esto debido a que el estado brindó información relativa a esta variable hasta determinada fecha, posteriormente no se dio más información al respecto.
Recta de mínimos cuadrados
La recta de aproximación por mínimos cuadrados del conjunto de puntos (X1, Y1), (X2, Y2)...(XN, YN) tiene la ecuación:
1.
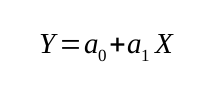
Donde las constantes a0 y a1 se determinan mediante el sistema de ecuaciones
2.
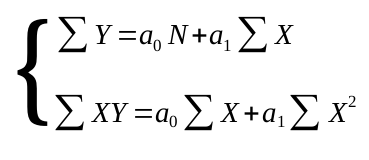
que son las llamadas ecuaciones normales para la recta de mínimos cuadrados (1).
Las constantes a0 y a1 pueden sacarse de (2), obteniéndose las fórmulas:
3.
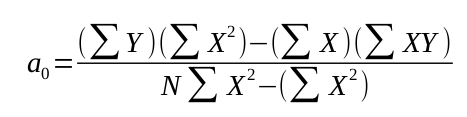
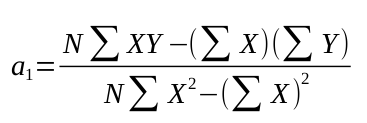
Las ecuaciones normales (2) se recuerdan fácilmente, observando que la primera ecuación puede obtenerse formalmente sumando en ambos miembros de (1), es decir, ΣY = Σ(a0 + a1X) = a0N + a1 ΣX, mientras que la segunda ecuación se obtiene formalmente multiplicando primeramente los dos miembros de (1) por X y después sumando, es decir, ΣXY = ΣX(a0 + a1X) = a0 ΣX + a1 ΣX 1. Nótese que esto no es una derivación de las ecuaciones normales, sino sencillamente una forma de recordarlas.
Nótese también que en (2) y (3) se ha empleado la notación ΣX, ΣXY, etc., en lugar de
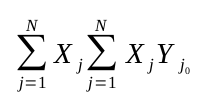
El trabajo necesario para encontrar una recta de mínimos cuadrados puede a veces simplificarse transformando los datos, de forma que x = X - X e y = Y - Y. La ecuación de la recta de mínimos cuadrados puede escribirse
4.
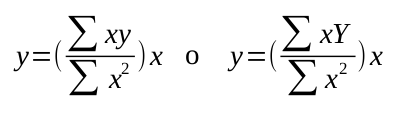
En particular, si X es tal que ΣX = 0, es decir, X = 0, se convierte en
5.
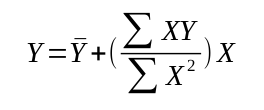
De estas ecuaciones se deduce inmediatamente que la recta de mínimos cuadrados pasa por el punto (X, Y) que es el centro de gravedad de los datos.
Si se toma como dependiente la variable X, en lugar de ser la independiente, se escribe (1) como X = b0 + b1 Y. Entonces, los resultados anteriores mantienen su valor si X e Y se intercambian y a0 y a1 se sustituyen por b0 y b1 respectivamente. Sin embargo, la recta de mínimos cuadrados resultante no es en general la misma que la obtenida anteriormente.
Relaciones no lineales
Las relaciones no lineales pueden reducirse a veces a relaciones lineales mediante una adecuada transformación de las variables.
Parábola de mínimos cuadrados
La parábola de aproximación de mínimos cuadrados a la serie de puntos (X1, Y1), (X2, Y2), ... (XN, YN) tiene la ecuación
6.
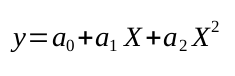
Donde las constantes a0, a1 y a2 se determinan resolviendo el sistema de ecuaciones
7.
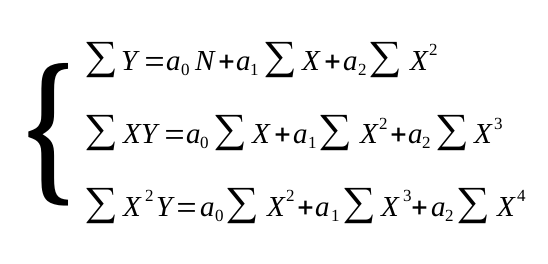
que son las ecuaciones normales para la parábola de mínimos cuadrados.
Las ecuaciones (6) se recuerdan fácilmente observando que se pueden obtener formalmente multiplicando la ecuación (5) por 1, X y X2, respectivamente, y sumando ambos miembros de las ecuaciones resultantes.
Como en el caso de la recta de mínimos cuadrados, las ecuaciones (6) se simplifican si X se elige de forma que ΣX = 0. También se obtiene simplificación eligiendo las nuevas variables x = X - X, y = Y - Y.
Regresión
A veces, basándose en los datos muestrales, se desea estimar el valor de una variable Y correspondiente a un valor dado de una variable X. ESto puede conseguirse estimando el valor de Y de la curva de mínimos cuadrados que ajusta los datos muestrales. La curva resultante se llama curva de regresión de Y sobre X, puesto que Y se estima a partir de X.
Si se desea estimar el valor de X a partir de uno dado de Y, se utiliza la curva de regresión de X sobre Y, que proviene de intercambiar las variables en el diagrama de dispersión de modo que X sea la variable dependiente e Y la variable independiente.
En general, la recta o curva de regresión de Y sobre X no es la misma que la recta o curva de regresión de X sobre Y.
Aplicaciones a series de tiempo
Si la variable independiente X es el tiempo, los datos muestran los valores de Y en diferentes tiempos. Los datos ordenados en relación al tiempo se denominan series de tiempo. La recta o curva de regresión de Y sobre X en este caso se llama frecuentemente recta de tendencia o curva de tendencia y se utiliza a menudo para fines de estimación, predicción o pronóstico.
Problemas que abarcan más de dos variables
Los problemas que abarcan más de dos variables son tratados de la misma forma que los de dos variables. POr ejemplo, puede existir una relación entre las tres variables X, Y y Z que puede venir dada por la ecuación
8.
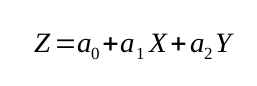
que se llama ecuación lineal entre las variables X, Y y Z.
Análisis de series de tiempo
Series de tiempo
Una serie de tiempo es un conjunto de observaciones hechas en momentos determinados, normalmente a intervalos iguales. Ejemplos de series de tiempo son la producción total anual de acero en Estados Unidos en un cierto número de años, el precio diario de cierre de una acción en la Bolsa, las temperaturas horarias anunciadas por el observatorio meteorológico de una ciudad y el total mensual de ventas habidas en un departamento de una tienda.
Matemáticamente, una serie de tiempo se define por los valores Y1, Y2,..., de una variable Y (temperatura, precio al cierre de una acción, etc.) en los momentos t1, t2... Así, Y es una función de t, simbolizada por Y = F(t).
Representación de series de tiempo
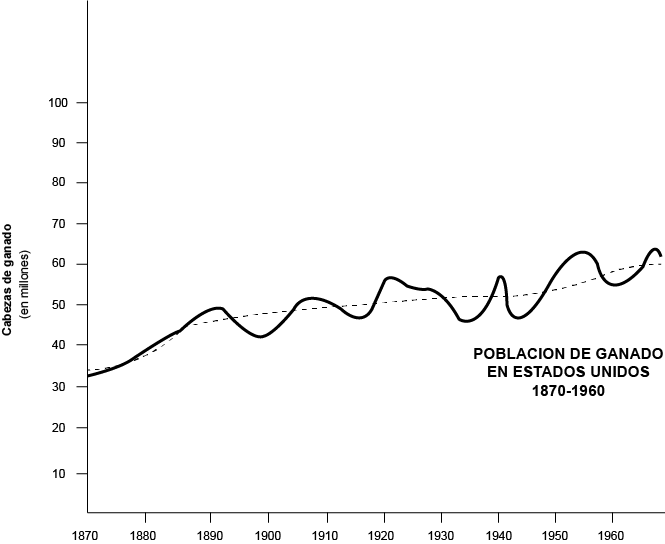
Una serie de tiempo que abarca a la variable Y, se representa costruyendo un gráfico de Y y t. La representación de una serie de tiempo mostrando la población de ganado en Estados Unidos durante los años 1870-1960 se da en la siguiente figura:
Movimientos característicos de las series de tiempo
Es interesante considerar el gráfico de una serie de tiempo, como descrito por un punto que se mueve con el paso del tiempo, en muchos aspectos análogo al movimiento de una partícula bajo la influencia de fuerzas físicas. Sin embargo, en lugar de fuerzas físicas, el movimiento puede ser debido a la combinación de fuerzas económicas, sociológicas, psicológicas u otras.
La experiencia basada en muchos ejemplos de series de tiempo ha revelado ciertos movimientos o variaciones características, algunos o todos ellos se presentan en diferentes grados. El análisis de tales movimientos es de gran importancia en muchos casos, uno de gran interés es el problema de la previsión de movimientos futuros. No es, pues, de extreañar que muchas industrias y acciones gubernativas están vitalmente unidas con tan importante materia.
Clasificación de movimientos de series de tiempo
Los movimientos característicos de una serie de tiempo pueden clasificarse en cuatro tiempos principales, llamados a menudo componentes de una serie de tiempo.
1. Movimientos seculares o de larga duración se refieren a la dirección general a la que el gráfico de una serie de tiempo parece dirigirse en un intervalo grande de tiempo. En el gráfico anterior, este movimiento secular o variación secular o tendencia secular como se llama a veces, se indica por una curva de tendencia, que aparece a trazos. En algunas series puede ser apropiada una recta de tendencia.
2. Movimientos cíclicos o variaciones cíclicas se refieren a las oscilaciones de larga duración alrededor de la recta o curva de tendencia. Estos ciclos, como se llaman a veces, pueden ser o no periódicos, es decir, pueden seguir o no exactamente caminos análogos después de intervalos de tiempo iguales. En negocios y actividades económicas, los movimientos se consideran cíclicos solamente si su período tiene un intervalo de tiempo superior al año. Un ejemplo importante de movimientos cíclicos son los llamados asuntos cíclicos, que representan los intervalos de prosperidad, retroceso, depresión y recuperación.
3. Movimientos estacionales o variaciones estacionales se refieren a las idénticas, o casi idénticas, normas que una serie de tiempo parece seguir durante los correspondientes meses de los sucesivos años. Tales movimientos se deben a sucesos recurrentes que se repiten anualmente, como, por ejemplo, los repentinos incrementos de ventas de un departamento antes de las Navidades.
Aunque los movimientos estacionales se refieren en general a una periodicidad anual en negocios o teoría económica, las ideas envueltas pueden extenderse a incluir una periodicidad de cualquier intervalo de tiempo, tal como diaria, horaria, semana, etc., dependiendo del tipo de datos que utilizan.
4. Movimientos irregulares o al azar se refieren a movimientos esporádicos de las series de tiempo debidos a sucesos ocasionales, tales como inundaciones, huelgas, elecciones, etc. Aunque normalmente se supone que tales sucesos producen variaciones que solamente duran un corto intervalo de tiempo, se concibe que pueden ser tan intensos que originen un nuevo ciclo u otros movimientos.
El análisis de series de tiempo
El análisis de series de tiempo consiste en una descripción (matemática generalmente) de los movimientos que la componen.
La figura (a) muestra el gráfico de una recta de tendencia secular o de larga duración (igualmente podría haber sido una curva de tendencia). La figura (b) muestra esta recta de tendencia de larga duración con un movimiento cíclico superpuesto (supuesto periódico). La figura (c) muestra un movimiento estacional superpuesto sobre el gráfico de la figura (b). Si se superpusiese sobre el gráfico (c) algún movimiento irregular o aleatorio, el resultado se asemejaría más a una serie de tiempo de las que en la práctica se presentan.
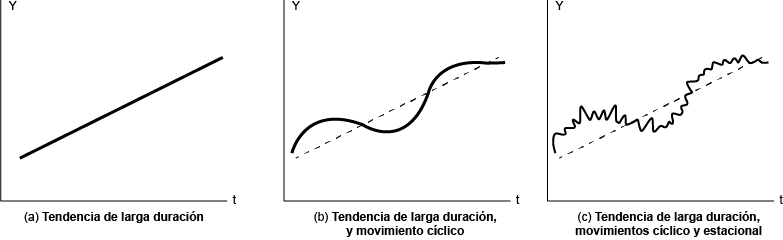
Las ideas anteriores suministran una posible técnica para analizar las series de tiempo. Se supone que en las series de tiempo la variable Y es un producto de las variables T, C S e I que originan, respectivamente los movimientos de tendencia, cíclicos, estacionales e irregulares. En símbolos,
Y = T x C x S x I = TCSI
El análisis de las series de tiempo consiste en una investigación de los factores T, C, S e I y a menudo se refiere a una descomposición de una serie de teimpo en sus movimientos componentes básicos.
Debe indicarse que algunos estadísticos prefieren considerar Y como suma T + C + S + I de las variables básicas que lo componen. Aunque en los métodos expuestos se supone la descomposición de (1), procedimientos análogos son aplicables cuando se supone Y como suma de sus componentes. En la práctica, la decisión sobre qué método de descomposición debe suponerse, depende del grado de éxito conseguido al aplicar el supuesto.
Movimientos medios, suavización de series de tiempo
Dado un conjunto de números
Y1, Y2, Y3,...
se define un movimiento medio de orden N al que viene dado por la sucesión de medias aritméticas,
9.
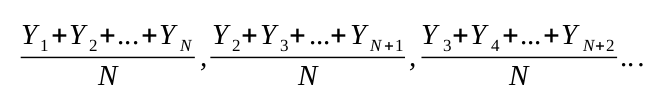
Las sumas de los numeradores de (9) se llaman movimientos totales de orden N.
Ejemplo 1: Dados los números 2,6,1,5,3,7,2 un movimiento medio de orden 3 está dado por la sucesión
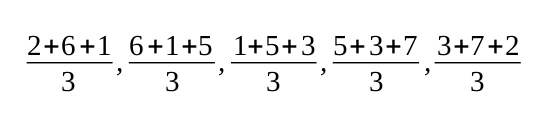
es decir, 3,4,3,5,4.
Se acostumbra a situar cada número del movimiento medio en su posición relativa apropiada con respecto a los datos originales. En este ejemplo se escribiría:
Datos originales: 2,6,1,5,3,7,2.
Movimiento medio de orden 3: 3,4,3,5,4.
Cada número del movimiento medio es la media de los 3 números inmediatos por encima de él.
Si los datos son dados anual o mensualmente, se llama movimiento medio de orden N a un movimienyo medio de N años o un movimiento medio de N meses, respectivamente. Así, se habla de movimientos medios de 5 años, movimientos medios de 12 meses, etc. Naturalmente que cualquier otra unidad de tiempo puede igualmente utilizarse.
Aplicación al caso Chile (PROYECCIONES)
Se muestran los modelos de regresión de series temporales y el método de medias móviles para la proyección de la pandemia en el caso Chile. A causa de la variación en los criterios por parte del estado para determinar las cifras de contagiados y fallecidos, se trabaja en la proyección de los fallecidos a través del método de medias móviles.
Impacto diario del COVID-19 en las defunciones en Chile
Artículo sacado de La Tercera.
"Las estadísticas muestran que en Chile mueren en promedio 290 personas al día. Especialista pondera el alcance que el Covid-19 podría tener en las estadísticas sanitarias
En el año 2017, de acuerdo al Anuario de Estadísticas Vitales que realiza el Instituto Nacional de Estadísticas (INE) en Chile murieron 106.040 personas, es decir, unas 290 personas al día. De ellas, el 27% fue a causa de enfermedades del sistema circulatorio, otro 26% a causa de algún tipo de cáncer y poco más del 10%, debido a enfermedades respiratorias.
Dicho de otro modo, por enfermedades del sistema circulatorio, fallecieron 28.591 personas, 78 personas al día. Por tumores malignos, fallecieron 26.229 personas, 71 personas cada día. Por enfermedades del sistema respiratorio, murieron 10.861, casi 30 personas cada 24 horas.
Los meses en que más personas murieron por esta causa fueron junio, julio y agosto, con 1.458, 1.391 y 1.129 respectivamente, meses en los que más virus respiratorio circulan en el ambiente.
De acuerdo al Departamento de Estadísticas e Información de Salud (DEIS) del Minsal, en el año 2016, de las 104.026, 3.166 personas lo hicieron a causa de neumonía y 77 por influenza.
Hoy, a causa de la pandemia por Covid-19,ya van 133 personas fallecidas y 10.507 confirmados positivos. ¿Cómo impactarán estas pérdidas de vida a la mortalidad del país? Desde marzo, cuando se confirmó el primer caso hasta ahora, en los 49 días en los que ha estado presente el virus, han muerto 2,7 personas por día."
Aplicación de las medias móviles en el caso Chile (FALLECIDOS)
Cuadro N° 1 - Media móvilBaja de medias móviles (FALLECIDOS)
Cuadro N° 2 - Media móvil (bajando)Estimado de fecha final de la pandemia en Chile
Artículo sacado de El Periscopio.
"En un estudio publicado por la Universidad de Tecnología y Diseño de Singapur, en conjunto con Data-Driven Innovation Lab, pudieron analizar las posibles fechas en las que se estará dando por terminada la pandemia por coronavirus en el mundo y en el país.
Gracias al desarrollo de un modelo que monitorea los casos confirmados por el virus, denominado SIR (susceptibles- infectados- recuperados) y el comportamiento de estos han podido dar con una fecha estimada.
'El modelo presenta datos de los diferentes países para estimar las curvas del ciclo de vida de la pandemia y predecir cuándo podría terminar en los respectivos países del mundo (...)', se puede leer en el sitio web del Laboratorio.
En el documento figura la fecha estimada para Chile donde para el 12 de julio la pandemia estará en un 97% controlada, y para el 1 de julio ya alcanzaría el 99%.
Lo que significaría que una recuperación total sanitaria por el Covid-19 estaría instaurándose de forma definitiva para el 2 de octubre próximo. "
Cabe destacar que el final de la pandemia dependerá completamente del seguimiento que realice la población a las normas recomendadas para prevenir la pandemia; si dichas normas son ignoradas, la pandemia puede expandirse y durar más de lo proyectado en el estudio.
Medias móvilesEn el siguiente sitio web se muestran las proyecciones de la pandemia a nivel mundial, utilizando la técnica del Machine Learning para la obtención de los datos. Click aquí
Ver estadísticas >>